RSA
RSA 암호 알고리즘은 공개키 암호시스템의 하나로, 전자 거래, 금융 거래, 인증서 등 다양한 분야에서 가장 보편적으로 사용되는 암호 및 인증 알고리즘입니다. RSA는 암복호화 과정에서 AES를 비롯한 대칭키 암호 알고리즘보다 훨씬 많은 연산을 필요로 합니다. 따라서 많은 데이터를 여러 번 암호화해야 하는 네트워크 통신에서는 잘 사용되지 않습니다. RSA는 알고리즘을 창시한 Rivert, Shamir, Adleman 3명의 이름을 따서 RSA 알고리즘이 만들어졌습니다.
예시)
1. 밥은 두 개의 소수를 고른 후 곱한다. ex) p=17,159, q=10,247 p * q = N = 175,828,273 -> 공개 열쇠
2. 앨리스는 밥의 공개 열쇠 N을 자신의 일방향 함수에 넣어서 계산한 뒤 밥에게 보낸다.
3. 밥은 p, q를 이용해 복호화한다.
중간에 이브가 N을 가로챘다면?? -> N이 10^130 크기 정도가 된다면 인수분해하는데 50년이 걸리므로 복호화는 불가능하다.
RSA 사전지식
모듈러 연산 분배법칙
(a + b) mod n = [(a mod n) + (b mod n)] mod n
a * b mod n = [(a mod n) * (b mod n)] mod n
a^x mod n = (a mod n)^x mod n
오일러의 정리
φ(n) -> n보다 작은 양의정수 중에서 n과 서로소인 수의 개수
만약 n이 소수이면 -> φ(n) = n - 1
만약 m, n이 각각 소수이면 -> φ(mn) -> φ(m) * φ(n) -> 이유 궁금하면 구글에 검색
a^φ(n) ≡ 1 (mod n) -> 조건: 양의정수 a은 n과 서로소
=> 위 식의 ≡는 합동으로 양쪽에 mod n을 하면 양쪽 값이 같다는 의미
ex) 4^100003 mod 33
-> φ(33) = φ(3) * φ(11) = (3 - 1) * (11 -1) = 20
100003 = 5000 * φ(33) + 3
4^100003 mod 33 => 4^(20 * 5000 + 3) mod 33 => 4^(20 * 5000) * 4^3 mod 33
=> [ 4^(20 * 5000) mod 33 * 4^3 mod 33] => [ 4^20 mod 33]^5000 * 4^3 mod 33
=> 1^5000 * 64 mod 33 => 31
확장 유클리드 알고리즘
ax + by = gcd(a, b) 를 만족하는 x, y가 하나 존재
a -> e, b -> φ(n) 이라면??
e ∗ x + φ(n) ∗ y = gcd(e, φ(n)) = 1 <= e와 φ(n)는 서로소이므로
e * d mod φ(n) = 1 <- x는 d이고 양변을 mod φ(n) 연산을 해도 같으므로
(e, n) is public key
d is private key
예시)
Choose two prime numbers p = 13 and q = 17
n = p*q = 221
φ(n) = (p − 1)(q − 1) = 192
choose e = 7 (7 is relatively prime to φ(n))
ed = 1 mod φ(n)
Solving the above equation is equivalent to: 7d + 192y = 1
Using extended Euclidean algorithm, we get d = 55 and y = −2
RSA 암호 알고리즘에서는 대칭키 암호와 달리 두 개의 키가 사용됩니다. 하나는 공개키(Public Key)로 모든 사용자에게 공개되며, 평문을 암호화할 때 사용됩니다. 다른 하나는 개인키(Private Key)로 타인에게 노출되어서는 안 되며, 공개키로 암호화된 암호문을 복호화할 때 사용됩니다. 공개키는 (n, e), 개인키는(n,d)로 표현할 수 있으며 송신자는 수신자의 공개키를 이용해 암호화를 하고 수신자는 개인키를 이용해 복호화한다.
RSA 암호화 복호화 과정

앨리스가 밥에게 암호문을 보내는 과정
1. 밥은 자신의 소수 p=2, q=7를 선택
2. n = p * q =14 -> n 값은 밥의 공개키가 됨
3. φ(n) = ( p - 1 ) * ( q - 1 ) => 1 * 6 = 6
4. φ(n)보다 작고 φ(n)와 서로소인 e 값 선택 => 1<e<6에서 5를 선택했다고 가정
5. (e * d)mod φ(n) ≡ 1 -> d = 11(5는 e와 같으므로 생략)
6. 공개키는 (14, 5), 개인키는 (14, 11)이다.
7. 앨리스가 밥의 공개키를 이용해 보낼 평문을 암호화(C: 암호문, M: 평문) -> C = (M ^ e) mod n => (평문 M은 3이라고 가정)
=> C ≡ (3 ^ 5) mod 14 = 5
8. 밥이 자신의 개인키를 이용해 앨리스가 보낸 암호문을 복호화 -> M ≡ (5 ^ 11) mod 14 = 3
RSA 공격
RSA 암호 알고리즘을 구현할 때, 빠른 암호화를 위해 공개 지수 e를 작게 설정하기도 합니다. 그러나 e를 너무 작게 설정하면 Coppersmith 공격과 Hastad's Broadcast 공격 등에 취약해질 수 있습니다.
Coppersmith 공격
Coppersmith 정리에 따르면, 차수가 e인 함수 f(x)에서 찾고자 하는 근이 n^{1/e}보다 작을 경우, 복잡도가 O(log\;n)인 알고리즘을 이용하여 근을 구할 수 있습니다.
Hastad's Broadcast 공격
이 공격은 한 송신자가 다수의 수신자에게 동일한 평문을 전송할 때, 수신자들에게 모두 동일한 작은 e 값을 사용할 경우 가능한 공격 방법입니다. 예를 들어, 공개키 을 가진 3명의 수신자들에게 같은 평문 을 암호화해서 보내는 경우를 생각해보면 수신자들은 서로 서로소인 n을 사용하고, 이를 로 표기하겠습니다. 각 수신자가 얻은 암호문을 라고 했을 때 아래 3개의 수식을 얻을 수 있습니다.
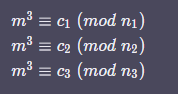
각 n이 서로 서로소이기 때문에 위 3개의 수식을 중국인의 나머지 정리를 이용해 합치면 아래의 수식을 얻을 수 있습니다.

여기서 각 n의 값이 모두 m보다 크기 때문에 m^3 <이 성립합니다. 따라서 위의 식에서 아래의 등식을 얻을 수 있습니다.
m^3
c는 위에서 중국인의 나머지 정리를 이용해 구한 값이므로 위 등식으로 평문 m을 구할 수 있습니다.
공개 지수가 작으면 이 두 개의 공격 외에도 Coppersmith의 짧은 패드 공격(Short Pad Attack) 등에 취약합니다. 그런데 그렇다고 공개 지수를 너무 큰 값으로 설정하게 되면, RSA 알고리즘의 효율성이 떨어지게 됩니다. 따라서 일반적으로는 공개 지수로 2^{16} + 1 = 을 사용합니다.
공통 사용
앞에서 설명했던 RSA의 공개 지수가 작을 경우 외에도 RSA를 공격하는 여러 공격 방법들이 존재합니다.
Common Modulus Attack
Common Modulus Attack은 같은 n과 서로소인 두 공개 지수 e1, e2를 사용하여 같은 평문을 암호화해서 두 암호문 을 만들었을 때, 이를 공격하는 기법입니다.
공격자는 두 공개 지수가 서로소라는 점을 활용해 r*e1 + s*e2 이고, 이 음수인 쌍을 확장 유클리드 알고리즘을 통해 구할 수 있습니다.
그 후 확장 유클리드 알고리즘을 사용해 c1^(-1)(mod n)을 구합니다.
계산된 값을 바탕으로 m을 구할 수 있습니다.
이처럼 수신자들이 같은 n을 사용하면 쉽게 공격받을 수 있습니다. 따라서 수신자들은 n을 무작위 값으로 생성하여 사용해야 합니다.
작은 d
비밀 지수 가 작아도 여러 공격에 취약합니다. d < (1/3) * 일 경우 Wiener's attack을 이용해 를 복구해 낼 수 있으며, Boneh Durfee attack를 사용하면 이보다 더 넓은 범위인 d < n ^ (0.292)일 경우에 를 복구해 낼 수 있습니다. 따라서 비밀 지수를 설정할 때는 보다 적당히 큰 수가 되도록 해줘야 합니다.
대칭키 암호와 공개키 암호의 큰 차이점 중 하나는 공개키(비대칭키) 암호는 어려운 수학 문제를 기반으로 하여 암호시스템의 안전성을 확보한다는 점입니다. 인수분해의 어려움을 기반으로 하는 RSA 외에도 이산대수의 어려움을 기반으로 하는 ElGamal 암호, 타원곡선 상에서의 이산대수의 어려움을 기반으로 하는 Elliptic Curve ElGamal 암호 등 다양한 공개키 암호 알고리즘이 존재합니다.
"문제의 어려움"을 기초로하는 이러한 공개키 암호 알고리즘들은 관련된 문제를 쉽게 풀수있게하는 알고리즘이 제시되거나, 컴퓨터의 연산 능력이 향상되면 안전성을 위협받게 됩니다. RSA의 경우, 양자 컴퓨터가 등장하면 쇼어 알고리즘으로 쉽게 풀릴 수 있다고 알려져있습니다. 그래서 암호학자들은 이런 미래를 대비하고자 양자 컴퓨터가 등장한 이후의 암호 시스템(Post Quantum Cryptography, PQC)에 대해서도 활발히 연구하고 있습니다.
'Cryptography' 카테고리의 다른 글
| [HackCTF] RSA3 (0) | 2021.10.16 |
|---|---|
| [AES 개념] (0) | 2021.10.12 |
| [HackCTF] Classic Cipher -3 (0) | 2021.10.09 |
| [HackCTF] Classic Cipher -4 (0) | 2021.10.06 |
| [HackCTF] RSA2 (0) | 2021.09.19 |



댓글